Comparison of information processing capabilities of two Fourier transform optical systems
Comparison of information processing capabilities of two Fourier transform optical systems
Ren Zhongjing
( Shandong Institute of Building Materials , Jinan , 250022)
Abstract: The different calculation methods of the spatial bandwidth product of the parallel light Fourier transform system and the convergent optical Fourier transform system are discussed. The relationship between the characteristics and the quantity of the two is compared. The calculation examples show that the spatial bandwidth product is optimized. The laser particle size analyzer has a central position in the design.
Key words : Fourier transform (FT) optical system; spatial bandwidth product; information processing capability
THE COMPARISON OF INFORMATION CAPACITY BETWEEN TWO KINDS OF FT OPTICALS SYSTEM
Ren Zhorigjing
(Shandong Institute of Building Materials)
Abstract: The different calculating methods of spatial-bandwidth between two kinds of FT optical system, parallel light and convergent light, have been discussed. A sample of calculation shows that it is important in design of laser particle sizer.
Key words: FT optical system; spatial-bandwidth; information capacity
introduction
The Fourier Transform (FT) optical system is a parallel information processing system and has important applications in many fields such as image processing, feature recognition, color coding, and particle analysis.
As an information processing system, information processing capabilities are of course the primary technical indicators. The information processing capability of an optical FT system is usually expressed by its spatial bandwidth product:

Where L is the object plane input size, Pm is the highest spatial frequency transmitted by the system, Pm = h/ λ F, h is the half height of the spectrum surface, λ is the wavelength of the light wave, and F is the focal length of the Fourier lens (or Equivalent focal length ) . Obviously, the information processing capability of the system is proportional to the input size and proportional to the highest spatial frequency of the output. The highest spatial frequency characterizes the resolution of the system's fine structure of the input two-dimensional image. The ability to resolve small particles.
Simply increasing the input size or increasing the detector area does not improve the information processing capability of the system. Limited by the aperture of the FT lens and also mutually constrained. This paper will provide a theoretical basis for the optimal design of high performance laser particle size analyzer by comparing the information processing capabilities of the parallel light FT system and the concentrated light FT system.
1 information processing capability of parallel light FT system
Conventional optical FT systems use parallel light illumination. Acronym parallel light FT system (Figure 1) was located at F. plane front focal plane of the lens T, located in the focal plane of the music score T F. After the lens. Let F. T lens aperture be D , focal length F , and incident light wavelength λ. From geometric optics, the highest spatial frequency at the point on the object axis is:

2 information processing capabilities of the concentrating FT system
It can be proved that the spherical wave illuminates the object surface, and the two-dimensional Fourier transform of the object plane image can also be obtained on the imaging surface. We call this imaging surface a spectral surface, and the distance from the object surface to the spectral surface is called the equivalent focal length.
Now we examine the information processing capabilities of the concentrating light FT system shown in Figure 2 . D1 point light source (or pinhole filter) FT lens to the distance, D2 is the distance from the lens to the object plane, D3 is the distance from the object plane to the music score, the lens aperture D.
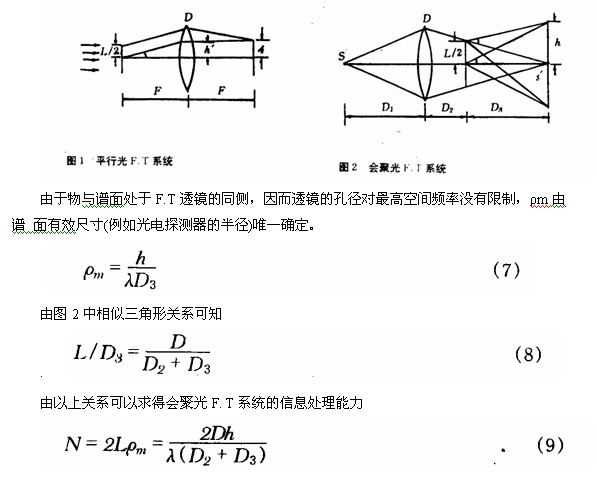
 Equation (9) indicates that the information processing capability of the system is proportional to the detector size , but it should be noted that excessive h will cause the symmetry of the diffraction spectrum to be destroyed and the error will increase. When h/D3 = 0. 15 , Î”Ï = 1.1% , and when h/D3 = 0.3 , Î”Ï = 4.6% .
Equation (9) also shows that the information processing capability of the system is independent of the equivalent focal length D3 , regardless of the distance between the object surface and the spectral surface. Change its spatial bandwidth product to a constant. The maximum input size Lm = D, which is double the optimal input size of the parallel light F. T system.
Equation (9) also shows that the information processing capability of the concentrating FT system is independent of the focal length F of the Fourier lens . This means making Different optical paths can be obtained by using different optical paths of the same lens , which undoubtedly increases the flexibility of information processing.
3 Comparison of two optical path information processing capabilities

In summary, the use of a full-concentration FT system has greater flexibility than a parallel-light FT system , properly selecting the detector size , and adjusting the imaging position can achieve a higher spatial bandwidth product than the parallel light system , that is, an increase. Information processing capabilities.
As an example of the application of the above theory, we analyze the spatial bandwidth product of the following two laser particle size analyzers. Table 1 gives specific data , where JL9000 is a parallel light F. T system and JL9200 is a converging light system.
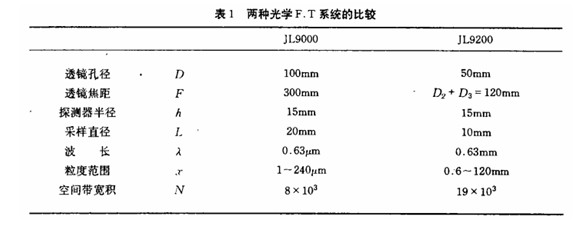
The data in Table 1 shows that JL9000 does not make full use of the potential of system optical information processing, so the space bandwidth product calculation can only make Use the formula (4) . The JL9200 chose the condenser optical path F. T system lens, although the aperture is reduced by 1/2 but the information processing capacity is more than twice as much as the former.
A portable high-resolution laser particle size analyzer designed using this study has obtained a utility model patent.
references
[1]Goodman J W. Introduction to fourter optics. McGraw - Hill, 1968
[2] VanderlugtA. Optical signal processing. John Wiley & Soans , Insc, 1992.
[3] according to any Chukyo laser, 1994,14 (1): 8--10. Â Â Â Â ,
SMART Digital Bluetooth Hearing Aids
SMART Digital Bluetooth Hearing Aids
Shenzhen Sunshine Technology Co.,Ltd , https://www.yatwinsz.com